
This can be determined by examining the t-test statistic. However, in some instances, the linearity of the linear relationship may not be appropriate. In most cases, linear regression is an excellent tool for prediction. The linear regression model is used to predict the value of a continuous variable, based on the value of another continuous variable. The t-test statistic helps to determine how linear, or nonlinear, this linear relationship is. The linearity of the linear relationship can be determined by calculating the t-test statistic. Why is a t-test used in the linear regression model? An example of multiple linear regression is Y = aX + bZ.
Multiple linear regression: Multiple linear regression is defined as linear regression with more than one predictor variable along with its coefficients. An example of a simple linear regression is Y = mX + b. 
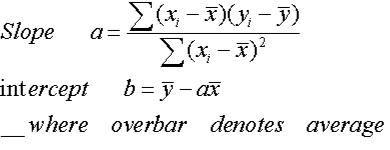

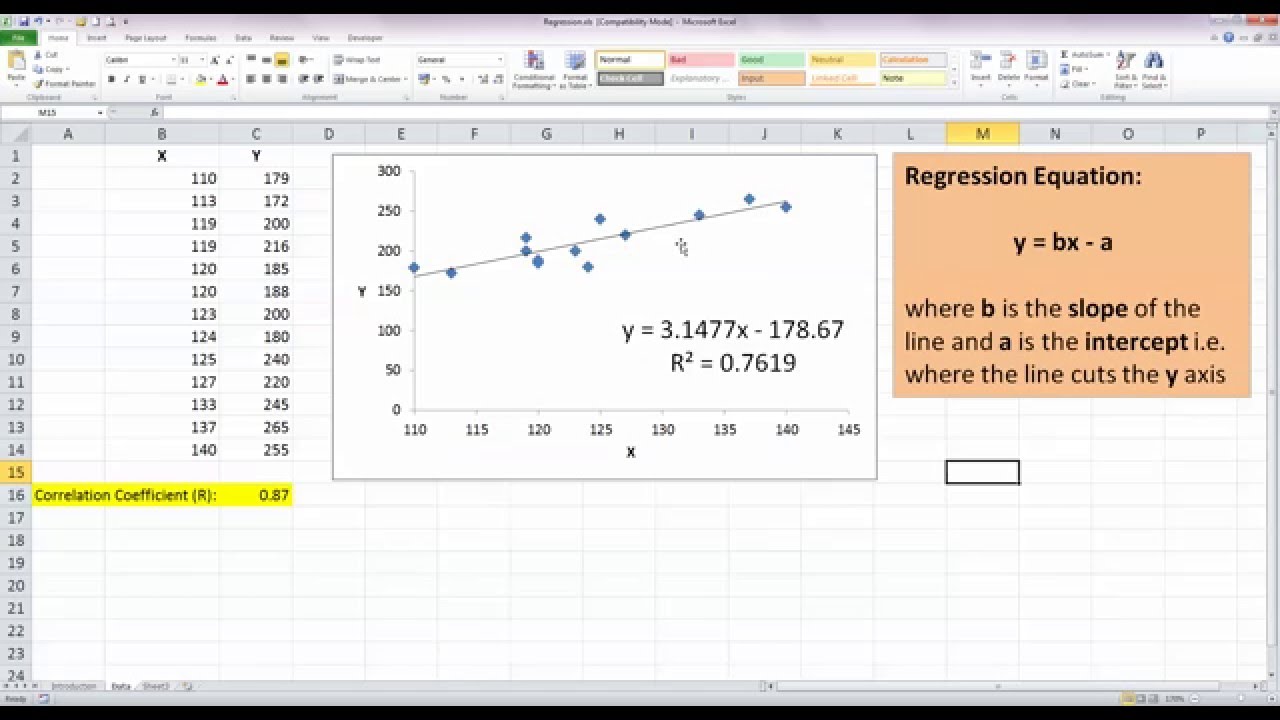
Simple linear regression: Simple linear regression is defined as linear regression with a single predictor variable. Linear regression is of two different types such as the following: The diagram below represents the linear regression line, dependent (response) and independent (predictor) variables. The linear slope, m, can also be termed as the coefficient of the predictor variable. Where Y represents the response variable or dependent variable, X represents the predictor variable or independent variable, m represents the linear slope and b represents the linear intercept. The linear regression line can be represented by the equation such as the following: It can as well be called the statistical linear model. A linear regression equation can also be called the linear regression model. In other words, it is a statistical technique that is used to determine if there is a linear correlation between the response and predictor variables. Linear regression is defined as a linear relationship between the response variable and predictor variables. Why is a t-test used in the linear regression model?.




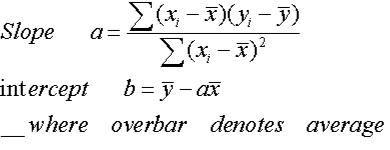



 0 kommentar(er)
0 kommentar(er)
